Shadows in computer graphics are the explicit handling of blocked light from surfaces — where other objects in the scene have occluded the light source during shading. To do this a test is done to see if the surface is directly visible to the light. This may take the form of a secondary ray–geometry intersection test between the surface and light sources or shadow maps can be used to pre-compute some visibility information for each light.
The first function of a renderer is to project the scene to an image and convert the geometry to pixel data. Basic lighting effects such as diffuse shading is another important feature. This operation can simply skip checking for obstacles between the surface and the light source, which would otherwise cause shadows to appear, applying lighting to everything. This is why shadows are considered to need explicit handling rather than than light not being there in the first place.
Diffuse shading makes surfaces facing a light bright and those facing away dark. It does not take the visibility of the light source into account. Since surfaces that face away from the light have zero light contribution this could be seen as implicit self shadowing but is not discussed as such.
A common mistake in shadow shaders is to darken the final color, or only partially scale down the direct light contribution when the shadows are too harsh. It is important to remember shadows are the absence of direct light. Ambient light is separate and back facing surfaces must match the color of the shadows. Following this principle will make multiple lights easier to implement and reduce the visual impact of artefacts such as shadow map precision errors.
Soft Shadows
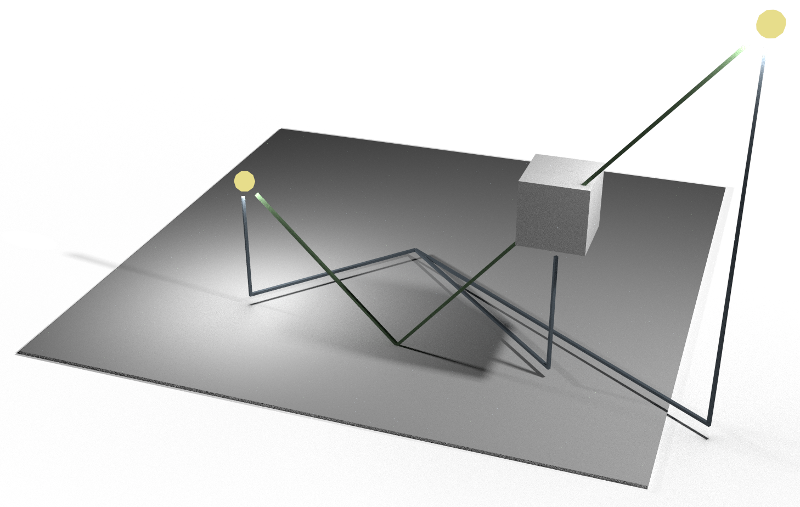
Soft shadows occur when a light source is bigger than a point, as pretty much all lights are. Shadows become blurred the larger the light source is and the further away the surface is from the occluding object. Some techniques simply blur the shadow, rather than correctly integrate the amount of light hitting each point on a surface.

To understand why shadows look blurry, imagine looking at the light source from a point on the surface. You can see an object partially covering the light. The amount of shadow is the ratio of light-area the object covers. To be more accurate, the amount of light the point receives is the sum/integral of all light across the remaining visible area. Now imagine moving around on the surface, still looking at the light. As you move from beneath the occluder more of the light is visible and the total intensity increases. This is why the edges of shadows have a smooth gradient. The problem is computationally very similar to depth of field rendering and techniques for each often apply to the other.
Raytracing
When shading a point, ray tracing the scene geometry from the point to the light position will tell you if there is anything in the way. If so, the point is in shadow and direct light contribution should not be applied. This isn’t practical for rasterizers and instead shadow maps are created to cache this query, but first we extend the ray concept to soft shadows.
A straight forward way to compute soft shadows when shading a surface is to use numerical integration. Light from all visible parts of light sources is summed by choosing lots of points on their surfaces and finding how many many are occluded. Another way of thinking of this is treating each point as a separate light source. Shading should really be applied for each point, but often they are so close together is it more efficient to integrate first and scale the overall light intensity, using a single centre point for the light direction. This approach is essentially that used in many raytracers.
Shadow Maps
Rasterizers are fast because they generate pixel data rather than search for ray–geometry intersections. This requires that the virtual viewing rays remain parallel in their projection. Rasterization is bad at computing arbitrary ray intersections such as secondary shadow rays. Instead, shadow maps can be used to pre-compute intersections between light rays and geometry. This is then queried during shading.
A shadow map is an image storing depth per-pixel, rendered from the point of view of a light. For the moment, assume the light is a spotlight with direction. A camera, or position, orientation and projection, is created for the light to match its direction. The scene is then rendered using this camera, but storing depth (distance to the camera) instead of colour in the image.

To find if a point is visible to the light, and not in shadow, it is transformed into the shadow map’s image space. If the point’s depth is greater than the value at that spot in the shadow map then something else is in the way and it is in shadow.
During shading the surface position is often used for lighting calculations. For example a position in eye space. This is transformed into the shadow map’s image space. In this case, $\mathsf{light}\mathsf{projection} \mathsf{light}\mathsf{view} \mathsf{camera}\mathsf{view}^{-1} \mathsf{position}$. This can be pre-multiplied so only a single matrix multiply is needed. Then, $\mathsf{shadow}\mathsf{position_{x,y}} < \mathsf{position}_z$ gives whether the surface is in shadow or not.
Due to precision errors and interpolation, banding is a common artefact where a surface casts a shadow on itself. To avoid this a depth bias, or offset, is added to the shadow map to err on the side of not in shadow: $\mathsf{shadow}\mathsf{position} + \mathsf{bias} < \mathsf{position}_z$.
